Could SPV Support a Billion Bitcoin Users? Sizing up a Scaling Claim

A new claim is being perpetuated in the bitcoin scaling debate.
We’re hearing that it is safe to remove the block size limit because bitcoin can easily scale to huge block sizes that would support billions of users via existing “simplified payment verification” (SPV) methods. Supposedly, SPV is very scalable due to the small amount of data it requires an SPV client to store, send and receive.
Let’s dig into this claim and examine it from multiple perspectives.
How SPV works
Satoshi described the high-level design for SPV in the bitcoin white paper, though it wasn’t implemented until two years later when Mike Hearn created BitcoinJ.
Early SPV implementations were quite naive – they downloaded the entire blockchain, which was no more efficient than a full node in terms of bandwidth.
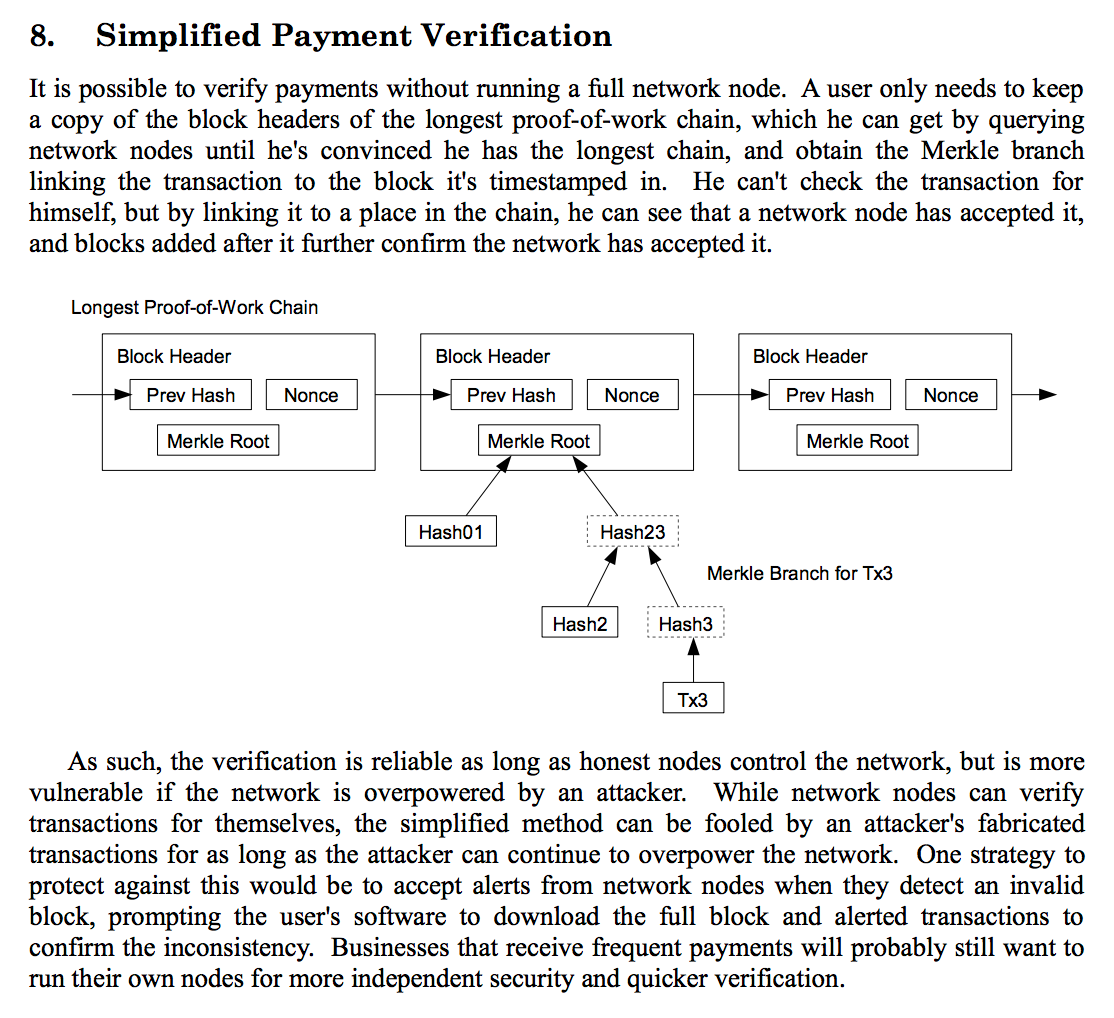
By throwing away transactions that weren’t relevant to the SPV client’s wallet, it was able to gain substantial disk usage savings. It took another 18 months for BIP 37 to be published, providing a specification for Bloom filtering of transactions, thus relying upon the block header’s Merkle root to prove inclusion of a transaction in a block as Satoshi had described. This provided greatly reduced bandwidth usage.
When an SPV client syncs with the bitcoin network, it connects to one or more fully validating bitcoin nodes, determines the latest block at the tip of the chain, then requests all of the block headers with a “getheaders” command for blocks from the last block it synced up to the chain tip.
If the SPV client is only interested in specific transactions corresponding to a wallet, it will construct a Bloom filter based upon all of the addresses for which its wallet owns private keys and send a “filterload” command to the full node(s) so that they know to only return transactions matching the filter.
After syncing block headers and possibly loading a Bloom filter, the SPV client sends a “getdata” command to request every single (possibly filtered) block they missed out on seeing since the last time they were last online, sequentially.
Once the client is in sync, if it remains connected to the full node peer(s) it will only receive “inv” inventory messages for transactions that match the loaded Bloom filter.
SPV client scaling
From a client’s point of view, Bloom filtering is a very efficient means to find relevant transactions in the blockchain, while using minimal CPU resources, bandwidth and disk space.
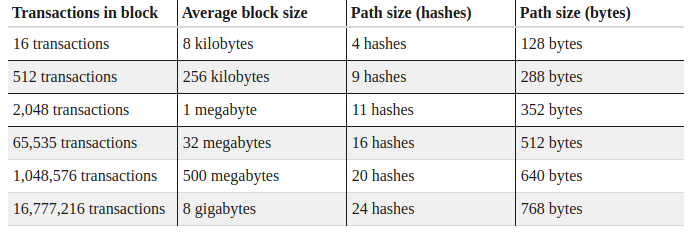
Every bitcoin block header is a mere 80 bytes, so at time of writing it’s only 38 megabytes of data for the entire eight-plus year history of the blockchain. Each year (roughly 52,560 blocks), only adds 4.2 megabytes, regardless of the size of blocks in the blockchain.
The Merkle tree that is used to prove inclusion of a transaction in a block also scales extremely well. Because each new “layer” that gets added to the tree doubles the total number of “leaves” it can represent, you don’t need a very deep tree in order to compactly prove inclusion of a transaction, even amongst a block with millions of transactions.
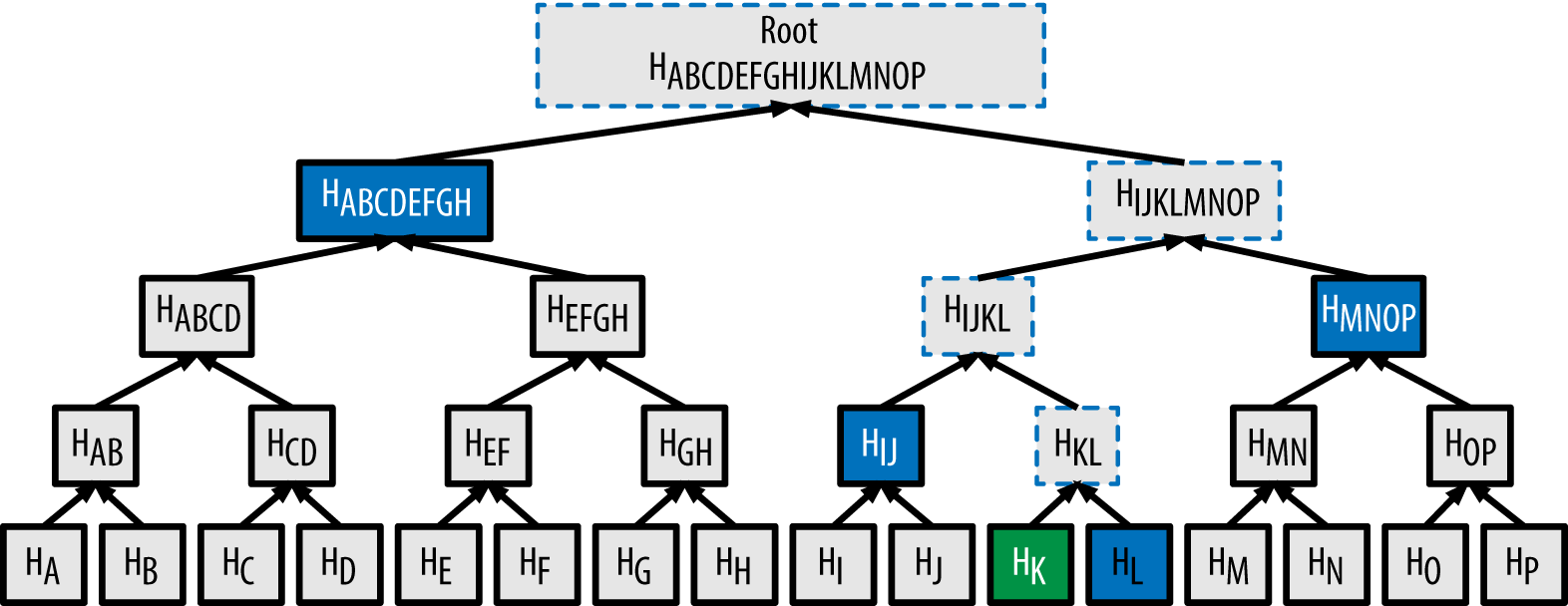
The Merkle tree data structure is so efficient that it can represent 16 million transactions with a depth of only 24 – this is sufficient to represent an 8GB block. Yet, the Merkle tree proof for such a transaction remains under 1KB in size!
It’s quite clear that from an SPV client perspective, the bitcoin network could be scaled to multi-gigabyte blocks and SPV clients would have little trouble processing the small amounts of data required – even on a mobile phone with a 3G connection.
But alas, scaling the bitcoin network is not nearly that simple.
SPV server scaling
While SPV is incredibly efficient for clients, the same does not hold true for the server – that is, the full node(s) to which SPV clients make requests. This method exhibits poor scalability for a number of reasons.
Nodes in the network have to process an extremely large amount of data to return the results for just a single peer, and they must repeat this work on every block for each peer that requests it. Disk I/O quickly becomes a bottleneck.
Every SPV client must sync the entire blockchain from the last time it had contact with the network, or, if it believes it missed transactions, it will need to rescan the entire blockchain since the wallet creation date. In the worst case, at time of writing, this is approximately 150GB. The full node must load every single block from disk, filter it to the client’s specifications and return the result.
Since blockchains are a form of append-only ledger, this amount will never stop growing. Without extensive protocol changes, blockchain pruning is incompatible with BIP 37 – it expects all blocks to be available at all full nodes that advertise NODE_BLOOM.
BIP 37 SPV clients can be lied to by omission. To combat this, SPV clients connect to multiple nodes (usually four) though it’s still not a guarantee – SPV clients can be partitioned off the main network by a Sybil attack. This increases the load on the network of full nodes by a factor of four.
For every connected SPV client that has been synchronized to the tip of the blockchain, each incoming block and transaction must be individually filtered. This involves a non-negligible amount of CPU time and must be done separately for every connected SPV client.
Crunching the numbers
At time of writing there are approximately 8,300 full nodes running that accept incoming connections; around 8,000 of them advertise NODE_BLOOM and should thus be capable of serving requests from SPV clients. But, how many SPV clients can the current number of listening full nodes reasonably support?
What would be required in order for the network to be comprised of full nodes that can support both a billion daily users and blocks large enough to accommodate their transactions?
Bitcoin Core defaults to a maximum of 117 incoming connections, which would create an upper bound of 936,000 available sockets on the network. However, the majority of these sockets are already consumed today.
Each full node connects to eight other full nodes by default. Bitcoin Core developer Luke-Jr’s (very rough) node count estimates 100,000 total nodes at time of writing; 92,000 of which don’t make sockets available for SPV clients. This eats up 800,000 available sockets just for full nodes, leaving only 136,000 sockets available for SPV clients.
This leads me to conclude that around 85 percent of available sockets are consumed by the network mesh of full nodes. (It’s worth noting that Luke-Jr’s estimation method can’t determine how much time non-listening nodes spend online; surely at least some of them disconnect and reconnect periodically.)
My node that powers statoshi.info averages 100 full node (eight outgoing, 92 incoming) peers and 25 SPV clients. That’s 80 percent of the available sockets being consumed by full nodes.
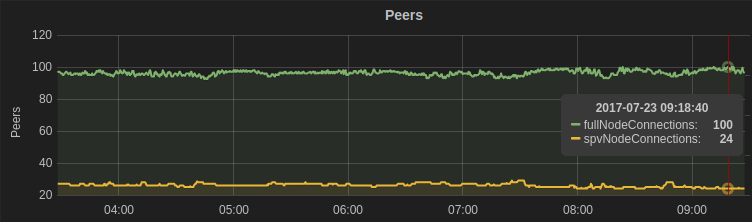
If we want even 1 billion SPV clients to be able to use such a system, there will need to be sufficient full node resources available to service them – network sockets, CPU cycles, disk I/O, and so on. Can we make the math work out?
In order to give the SPV scaling claims the benefit of the doubt, I’ll use some conservative assumptions that each of the billion SPV users:
– Send and receive one transaction per day.
– Sync their wallet to the tip of the blockchain once per day.
– Query four different nodes when syncing to decrease chances of being lied to by omission.
A billion transactions per day, if evenly distributed (which they surely would not be) would result in about 7 million transactions per block. Due to the great scalability of Merkle trees, it would only require 23 hashes to prove inclusion of a transaction in such a block: 736 bytes of data plus an average 500 bytes for the transaction.
Add another 12KB worth of block headers per day and an SPV client would still only be using about 20KB worth of data per day.
However, 1 billion transactions per day generates 500GB worth of blockchain data for full nodes to store and process. And each time an SPV client connects and asks to find any transactions for its wallet in the past day, four full nodes must read and filter 500GB of data each.
Recall that there are currently around 136,000 sockets available for SPV clients on the network of 8,000 SPV-serving full nodes. If each SPV client uses four sockets, then only 34,000 clients can be syncing with the network at any given time. If there were more people online at once than that, other users trying to open their wallet would get connection errors when trying to sync to the tip of the blockchain.
Thus, in order for the current network to support 1 billion SPV users that sync once per day, while only 34,000 can be syncing at any given time, that’s 29,400 “groups” of users that must connect, sync, and disconnect: each user would need to be able to sync the previous day of data in less than three seconds.
This poses a bit of a conundrum because it would require each full node to be able to read and filter 167GB of data per second per SPV client continuously. At 20 SPV clients per full node, that’s 3,333GB per second. I’m unaware of any storage devices capable of such throughput. It should be possible to create a huge RAID 0 array of high-end solid state disks that can achieve around 600MB/s each.
You’d need 5,555 drives in order to achieve the target throughput. The linked example disk costs $400 at time of writing and has approximately 1TB of capacity – enough to store two days’-worth of blocks in this theoretical network. Thus, you’d need a new array of disks every two days, which would cost you over $2.2 million – this amounts to over $400 million to store a year’s-worth of blocks while still meeting the required read throughput.
Of course, we can play around with these assumptions and tweak various numbers. Can we produce a scenario in which the node cost is more reasonable?
Let’s try:
What if we had 100,000 full nodes all running cheaper, high-capacity spinning disks and we somehow convinced them all to accept SPV client connections? What if we also managed to modify the full node software to support 1,000 connected SPV clients?
That would give us 100 million sockets available for SPV clients that could support 25 million simultaneous SPV clients on the network. Thus each SPV client would have 2,160 seconds per day to sync with the network. For a full node to keep up with demand it would need to maintain a consistent read speed of 231MB/s per SPV client, which would result in 231GB/s assuming 1,000 connected SPV clients.
A 7,200 RPM hard drive can read about 220MB/s, so you could achieve this read throughput with a RAID 0 array of a bit more than 1,000 drives.
At time of writing you can purchase a 10TB drive for $400, thus a $400,000 RAID array of these drives would enable you to store 20 days’-worth of blocks – this amounts to a much more manageable $7.2 million to store a year’s-worth of blocks while still achieving the disk read throughput requirements.

You’ll need to add at least 2 of these every day!
It’s worth noting that no one in their right mind would run a RAID 0 array with this many drives because a single drive failure would corrupt the entire array of disks. Thus a RAID array with fault tolerance would be even more expensive and less performant. It also seems incredibly optimistic that 100,000 organizations would be willing to pony up millions of dollars per year to run a full node.
Another point to note is that these conservative estimates also assume that SPV clients would somehow coordinate to distribute their syncing times evenly throughout each day. In reality, there would be daily and weekly cyclical peaks and troughs of activity – the network would need to have a fair higher capacity than estimated above in order to accommodate peak demand.
Otherwise, many SPV clients would fail to sync during peak usage hours.
Interestingly, it turns out that changing the number of sockets per node doesn’t impact the overall load on any given full node – it still ends up needing to process the same amount of data. What really matters in this equation is the ratio of full nodes to SPV clients. And, of course, the size of the blocks in the chain that the full nodes need to process.
The end result appears inescapable: the cost of operating a full node capable of servicing the SPV demand of a billion daily on-chain transactors would be astronomical.
Seeking a middle ground
By this point, it’s quite clear that a billion transactions per day puts the cost of operating a fully validating node outside the reach of all but the wealthiest entities.
But, what if we flip this calculation on its head and instead try to find a formula for determining the cost of adding load to the network by increasing on-chain transaction throughput?
In order for the bitcoin network to support a target number of transactions per second (adding capacity for 86,400 net new daily users), we can calculate the per-node disk throughput requirements as:

This gives us the minimum disk read throughput per second for a full node to service demand from SPV clients. With the existing characteristics of the network and available technology, we can extrapolate an estimated cost of node operation by using disk throughput as the assumed bottleneck. Note that there are surely other resource constraints that would come into play, thus increasing the cost of full node operation.
For the following calculations, I used these assumptions:
– Average transaction size in bytes = 500 bytes based upon statoshi.info.
– Total number of SPV users = one per transaction per day.
– Sockets consumed by an SPV client = standard of four.
– Number of sockets available for SPV clients on each full node = prior calculated number of 20.
– Total network sockets available for SPV clients = prior calculated number of 136,000.
– Cost of hard drive throughput and space = $400 10TB 7,200 RPM drives in RAID 0 configuration.
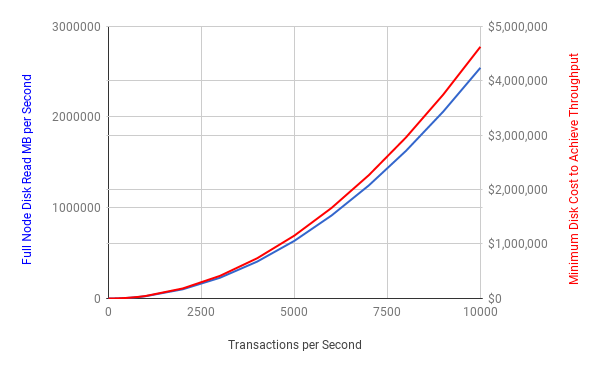
We can see that in terms of disk throughput it stays fairly reasonable until we surpass 100 transactions per second. At that point you start having to buy multiple disks and stripe them in a RAID array in order to achieve the performance requirements.
Unfortunately, the disk throughput requirements and thus cost to operate a full node increase quadratically in relation to the number of transactions per second. The costs quickly become untenable for most entities.
For reference, recall that Visa processes about 2,000 transactions per second. On bitcoin this would require nearly $200,000-worth of disks just to keep up with SPV demand. One point worth noting is that these charts keep the number of full nodes constant at 8,000 – in reality, they would likely decrease as the cost went up, thus raising the throughput requirements and cost of operating the remaining nodes to increase even faster.
This appears to be a compounding force of node centralization.

As I concluded in “How to Save Bitcoin’s Node Network From Centralization“, one of the root issues of contention around increasing the block size is the cost of node operation. The above calculations give us a glimpse of the complexities of calculating the cost of node operation because there are so many variables involved – these calculations were keeping most of the variables constant and only focusing on disk I/O cost.
The (unscientific) polls I ran a year earlier showed that 98% of node operators would not pay more than $100 per month to run a node, even if they were highly invested in bitcoin. I’d be willing to bet that increasing bitcoin’s on-chain transactions by an order of magnitude would result in the loss of a majority of full nodes, while an increase of two orders of magnitude would result in a loss of 90% or more nodes.
I believe it’s safe to assume that very few entities would be willing to go to the trouble of building RAID arrays in order to run a full node. If this is the case, it’s untenable to claim that such increases would be fine for the average user, because there wouldn’t be nearly enough full node disk throughput or sockets available to service SPV demand.
Other SPV weaknesses
SPV is great for end users who don’t require the security or privacy of a fully validating node. However, there are plenty of reasons that could be considered showstoppers for a mostly-SPV bitcoin network, regardless of its scalability.
SPV makes major assumptions that result in it having weaker security and privacy than a fully validating node:
- SPV clients trust miners to correctly validate and enforce the rules of bitcoin; they assume that the blockchain with the greatest cumulative proof-of-work is also a valid chain. You can learn about the difference between SPV and full node security models in this article.
- SPV clients assume that full nodes will not lie to them by omission. A full node can’t lie and say that a transaction existed in a block when it didn’t actually exist, but it can lie by saying that a transaction that does exist in a block did not happen.
- Because SPV clients strive for efficiency, they only request data for transactions belonging to them. This results in a massive loss of privacy.
Interestingly, the co-author of BIP 37, Matt Corallo, regrets creating it:
“A big issue today for privacy of users in the system is BIP37 SPV bloom filters. I’m sorry, I wrote that.”
BIP 37 Bloom-filtered SPV clients have basically no privacy, even when using unreasonably high false-positive rates. Jonas Nick [a security engineer at Blockstream] found that given a single public key, he could then determine 70% of the other addresses belonging to a given wallet.
You could work around SPV’s poor privacy by splitting Bloom filters among many peers, though this would make the scalability of SPV even worse by placing more load on more full nodes.
BIP 37 is also vulnerable to trivial denial-of-service attacks. Demonstration code is available here that is able to cripple full nodes by making many fast inventory requests through specially constructed filters that cause continuous disk seek and high CPU usage.
The author of the attack’s proof-of-concept, Core Developer Peter Todd, explains:
“The fundamental issue is that you can consume a disproportionate amount of disk I/O bandwidth with very little network bandwidth.”
Even to this day, the fraud alerts that Satoshi described in the white paper have not been implemented. In fact, research efforts in this area have shown it may not even be possible to implement lightweight fraud alerts.
For example, a fraud alert only works if you can actually get the data required to prove fraud – if a miner does not provide that data, the fraud alert can’t be created. As such, SPV clients don’t have the level of security that Satoshi envisioned they would have.
From a very high-level perspective, a world consisting mostly of SPV nodes makes consensus changes such as the total coin cap or even editing of the ledger much easier. Fewer fully validating nodes means more centralized enforcement of consensus rules and thus less resistance to changing consensus rules. Some people may consider that a feature; most surely consider it a flaw.
Potential improvements
SPV security & scalability could potentially be improved in a number of ways via fraud proofs, fraud hints, input proofs, spentness proofs, and so on. But as far as I’m aware none of these are past the concept phase, much less ready for production deployment.
Bloom filter commitments could improve privacy, but there’s a tradeoff for usefulness between the size of the filter and its false positive rate: too coarse means peers download far too many false-positive blocks, too fine means the filters will be absolutely gigantic and impractical for anybody to download with an SPV client.
It would reduce the load on full-node disk throughput, but the trade-off would be increased bandwidth by both SPV clients and full nodes because entire blocks would have to be transferred across the network.
This recently proposed compact client-side filtering eliminates privacy issues, but it does require full blocks to be downloaded if there is a match against the filter (though not necessarily via the p2p network!).
UTXO commitments could enable SPV clients to sync their current UTXO set and thus wallet balance without requiring the full node to scan the entire blockchain. Rather, it would provide a proof of the UTXOs existing.
It may be possible to guard against Bloom filter DoS attacks by requiring SPV clients to either submit proof-of-work (untenable on a battery-powered device like a phone) or channel-based micropayments (impossible to bootstrap if a client hasn’t received money yet), but neither offers a straightforward solution.
The disk read requirements for full nodes could likely be reduced in a number of ways via improved indexing of data and batched processing of requests from SPV clients.
Ryan X Charles pointed out in the comments below that using BIP70’s payment protocol to directly tell someone the UTXO id of the payment you’re sending them would remove the need for them to use bloom filters at all since they could request the data directly from full nodes. This is incredibly efficient if you’re willing to accept the privacy trade-off.
Suffice to say, there is plenty of room for improvement – many challenges will need to be overcome in order to improve on-chain scalability.
Suitable scaling solutions
If we ignore the multitude of miscellaneous other issues with scaling to larger block sizes such as block propagation latency, UTXO set scaling, initial blockchain syncing times and security and privacy trade-offs, it may be technically possible to scale bitcoin to a billion daily on-chain users if there are entities willing to invest significant resources to develop software improvements and to operate the required infrastructure.
It seems highly unlikely that bitcoin would evolve organically in that fashion, however, because there are much more efficient ways to scale the system. The most efficient is a form of scaling already being used: consolidation around centralized API providers. There tend to be huge trust and privacy trade-offs when employing these methods, but many such interactions involve contractual agreements that mitigate some of the dangers.
In terms of scaling in a trustless manner, Layer 2 protocols such as Lightning offer much more efficient scaling because the high volumes of data being transferred are only being sent amongst the small number of parties directly involved in a given off-chain transaction. You can think of it as the difference between a broadcast-to-all ethernet communication layer versus a routed IP layer – the internet couldn’t scale without routing and neither can the Internet of Money.
While this approach to scaling is much more technically complex than traditional centralized scaling and will require overcoming some unique challenges, the up-front investment of resources for research and development of these routing protocols will pay huge dividends over the long term, as they reduce the load that needs to be borne by the entire network by orders of magnitude.
There are also plenty of options in between that can be explored:
– Centralized custodial schemes with perfect privacy that use Chaum tokens such as HashCash.
– Centralized non-custodial zero knowledge proof systems such as TumbleBit.
– Federated (semi-trusted multisignature) sidechains.
– Miner-secured (semi-trusted) drivechains.
I’m still convinced that in the long term, bitcoin will need much larger blocks.
But let’s be patient and tactful by trying to scale the system as efficiently as possible while maintaining its security and privacy properties.
An auditable, slightly decentralized PayPal would surely have utility if it was functional from the standpoint of the average user, but it would not offer the level of financial sovereignty that bitcoiners enjoy today.
Thanks to Matt Corallo, Mark Erhardt and Peter Todd for reviewing and providing feedback for this article